In the fall of 2011, the University of Waterloo Computer Science Club organized their artificial intelligence (AI) challenge for the fourth time. The goal of the challenge is to write a computer program (a so called bot) that solves an simple to explain, yet hard to solve problem as good as possible. Below, I explain the challenge and discuss my bot, with which I finished 53rd out of 7897.
Rules
In this edition of the AI challenge, the game was called Ants. A full description of it can be found on the official website, but I’ll try to give a concise version here.
Each player starts with one or more ant hills on an unknown map together with a number of other players. On each ant hill an ant is spawned which can be controlled by the player’s bot. By moving the ant, which has a limited area of vision, bots can explore the map and find randomly spawned food. Parts of a map can be blocked off by impassable water tiles. Maps wrap around top to bottom and right to left. Picking up a piece of food will spawn a new ant on one of the player’s ant hills. If an enemy ant walks over an ant hill, that hill is destroyed. When ants of multiple players meet, a rule based on the concentration of ants decides which ants die and which live. The goal is get the highest score by destroying as many enemy ant hills as possible. The game ends when only a single player has any hills left or when a time limit is reached.
All games are played completely by bots, there is no human interaction possible. The AI challenge allows bots to be coded in over 25 different programming languages. I chose to use C++11, due to its flexibility and speed. This proved to be critical in the final versions of my bot, when I had to optimize in order to stay below the allowed calculation time of 500 ms per round. OO programming and templates where definitely a big help in getting this done.
So, with all that said, let’s dive into the inner workings of my bot. I should mention that a lot of the ideas and insights that went into putting this bot together were gained from discussions on the official website’s forum.
One final note: in the images below, blue tiles are impassable water tiles, circular objects are ants (colored per player, orange for my bot), square objects are food, and the brown structures are ant hills.
Path planning
Being able to efficiently plan the movement of all ants is without a doubt the most important part of any bot. On large maps, with an efficient bot, it’s possible to have over 200 ants. Ideally, a bot should be able to decide on a goal for each ant and calculate the best path towards that goal every single turn, in less than the allowed 500 ms.
There are huge number of options for path planning. There’s “intelligent” algorithms, such as Dijkstra’s algorithm and A*, especially about the latter a tons of research papers are available on how to improve and tweak the algorithm for specific use-cases. Even “dumb” algorithms, such as BFS, work extremely well in this case, in fact multiple bots in the final top 10 used it.
Path planning is only part of the problem, however. In order to be able to plan a path, the bot first needs to decide on a goal for each ant. Hoping to kill two birds with one stone, I opted to use potential field diffusion for both goal selection and path planning. The easiest way to visualize potential field diffusion is as a scent spreading out over an area. Initially, the scent will be contained to a small area, but as time progresses, areas further away will start smelling stronger and stronger, as long as the source of the scent remains present. An example of diffusion for food tiles is shown in the image below, you can see how the field spreads out from the solid green food tiles. The brown colored food tiles have not yet been detected by the bot (due to limited vision range of the ants).
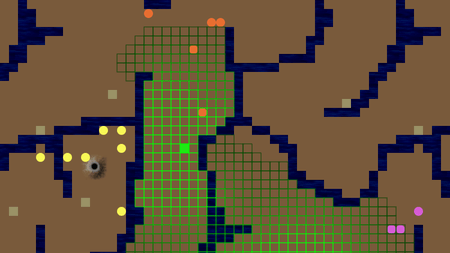
The bot keeps track of the diffusion maps for: food, exploration, enemy ants & enemy hills. It assigns a fixed potential to food, tiles just beyond the edge of vision (exploration), enemy ants & enemy hills. Food is scored higher earlier in the game, while unseen tiles are scored higher the longer they have been unseen. Both food & enemy hills get a lower potential the longer it has been since my ants have seen them. Enemy ants get a higher value the closer they get to one of my hills, limited to a minimum value. All potentials are calculated using an exponential decay function: in every iteration of the diffusion function each tile that hasn’t got a fixed potential gets as its new potential value an exponentially weighted sum of nearby tiles.
The spread of potential values is attenuated if one of my ants is on a tile. Depending on the type of field, this attenuation is high or low. When calculating the food potential field for example, an ant will block 99.99% of the potential, while for the enemy hills field this is only 10%. One problem with diffusion is that it doesn’t work too well when there are a lot of small passages. So to fix this, while diffusing, the value of a tile is scaled proportionally with the number of neighboring water tiles. This fix improved my bot quite a lot on maps with narrow tunnels. Before putting this in, the bot would ignore food in these small tunnels, since their potential couldn’t spread out.
Calculating the shortest path to a goal is a simple matter of going to the closest nearby tile with the strongest potential field. However, every call to the diffusion function the potential fields only spread out one tile. Thus, the diffusion function should be called plenty of times, the more the better. My bot tries to execute around 180 diffusions each round, which takes an amount of time dependent only on the size of the map. Thus, since the calculation time is completely independent of the number of ants, the potential field diffusion method for path planning is very inefficient for a small number of ants, but becomes very interesting once the bot needs to move hundreds of ants.
An extra benefit of this method is that you don’t have to worry about exceeding the allowed calculation time, since the diffusion calculation time is fixed. Compare this with most of the other path planning algorithms, where each ant has its path planned separately. Those other algorithms might exceed the total allowed calculation time when the bot needs to control a large number of ants, since the total time in that case is linear in the number of ants.
Goal planning
As stated above, following the shortest path to a goal means simply following the trail with the highest potential field value. However, the bot keeps track of four different potential fields (food, exploration, enemy ant, and enemy hills), so the problem arises of choosing a field to follow.
What I do is calculate the sum of potentials (food + exploration + enemy ant) and then move each ant to the nearest reachable tile with the largest value. You might have noticed that the enemy hill potential field is not included in the sum. Ants ignore this field, except when they are marked as attack ants in which case they follow the potential field (food + enemy ant + enemy hill). Every ant is marked with a role according to which of the fields used in the summation is the strongest at that point. A large amount of time was spend tweaking the relative strength of the potential fields, such that the bot would make reasonable goal decisions, e.g. don’t sent an ant off to the other side of the map to explore if there’s a food tile ten steps away.
Marking an ant as an attack ant is done each turn by selecting the 50% of ants with the largest enemy hill potential field at their location. In case no enemy hill is detected, no ants are marked as attack ants. The 50% is an arbitrary number that seemed to work well, finding a more optimal method of deciding on a number of ants to select only lead to worse performing bots.
The bot also detects which ants are in a combat situation, i.e. close to enemy ants. A CombatManager class calculates decisions for these ants, how it does this is described further on. For combat ants, I distinguish between safe tiles (where my ants are certain to kill an enemy) and nocombat tiles (where no combat can take place, so ants are also safe). The sum of potentials of a nocombat tile is only 20% of its true sum value, so ants will prefer moving to safe tiles. This has the effect that they prefer killing an enemy over running away. For combat ants that have neither safe nor nocombat tiles nearby, the movement direction does not matter, since they will die anyway.
The sums for all directions for each ant are then sorted in descending order, the bot then loops over each option and checks if the best unchecked move is safe to execute according to my combat manager (i.e. the ant won’t die when it moves there, unless it’s allowed to suicide). If an ant wants to move to the location of another ant, I push the first ant on a stack to evaluate later and check the other ant first. This ensures that I can not have any collisions, which would lead to the suicide of both colliding ants.
There are a few extra tweaks here and there, such as an idea I got while reading delineate’s explanation of his bot: reduce the sum of potentials of tiles that border water tiles. I had noticed that often, when running away from enemies, my ants would get themselves stuck near water. So, for every neighboring water tile, the sum of potentials of a tile is reduced by 5%, which leads the ants to prefer tiles away from it.
In the image below, you can distinguish between the four potential fields: green for food, yellow-ish for exploration, red-ish for enemy hills, teal for enemy ants. The role of each of my ants is marked with a circle of the same color around them. Combat ants have a red dot in their center.

Combat
The second important aspect of a bot, and one which sets apart the so-so from the good bots, is combat management. In order to better understand the way my combat manager works, lets first take a look at the combat rule. Each ant has a combat radius around it, when an enemy ant comes within this radius, both ants are in combat modes. Whether an ant lives is decided based on the following rule:
for (enemy : ant.getEnemiesInRange()) {
if (ant.numEnemiesInRange() >= enemy.numEnemiesInRange()) {
ant.dead = true;
break;
}
}Although the rule is simple, calculating the movements which statistically minimize the death of your ants and maximize those of the enemy ants, while staying below the maximum 500 ms calculation time, is very hard. I wrote a program that did this, but it was too slow. Especially when during one turn multiple combat zones with more than 10 ants each exist, it was impossible to use such an algorithm. Therefore, a much faster heuristic solution is needed.
My initial combat logic worked by modifying potential field values locally depending on the number of nearby friendly and enemy ants. This worked OK, but could not beat the better bots in combat. I then tried the aforementioned method of statistically optimal movements, which was way too slow. When that failed, I spend some time on an approach based on neural networks (NN), which where trained using statistically optimal movements. Unfortunately, I couldn’t get any decent output from the NN. Luckily for me, the author of one of the top bots (Memetix) posted his combat method on the official forum, so I restarted from scratch and based my combat routines on his idea.
The general idea is to act as if each ant can move to every neighboring tile the next turn. For each player a array is then generated which keeps track for each tile of how many ants have that tile within their combat radius. Based on these numbers, it is possible to calculate which tiles are safest and how strong the strongest ant of each player in a certain region is. Of course this is an approximation, since it assumes that ants can be in multiple locations at once. Despite that, this algorithm works very well.
I build upon this idea and added some extra features. First of all, after I decide where to move a combat ant, I fix that ant at its new position in the combat manager. Then, I reevaluate the combat for the remaining ants. This helps when the success of a move is dependent on where nearby ants move to. Doing this improved combat quite a bit, since it makes accidental suicide happen a lot less often (i.e. an ant would move to a tile assuming it was safe, which was only the case if another ant moved in the same direction as well).
What I also did was detect when attack ants (those that are trying to destroy an enemy hill) are blocked by enemy ants. If at least 70% of them are blocked, I allow them to suicide as long as they kill at least 1 enemy ant. To calculate this correctly however, you need to know not how strong the strongest nearby enemy ant is, but how weak the weakest one is.
Now a problem arises when fixing an ant at its position. Without knowing how many enemies each enemy ant has on a tile, you can not correctly update the strongest and weakest enemy values without recalculating everything. To fix that, instead of storing just the strongest and weakest values per tile, I keep a priority queue for each tile in a combat zone to keep track of how many enemies each enemy ant has to fight in that tile. When an ant’s position is fixed, the priority queues for ants on tiles which won’t be in the moved ant’s combat radius anymore are updated.
Finally, I also detect stationary enemies. An enemy is regarded as stationary if he hasn’t moved for at least 10 turns in a row. When this happens, that enemy’s position is fixed during the combat evaluation. This helps to detect better moves during stalemates and allows suiciding my ants more efficiently while trying to destroy an enemy hill.
Below an image is shown of some very nice emergent behavior during combat, i.e. behavior that is not specifically implemented, but is due to interactions within the AI. You can see my ants surrounding the enemy (pink) ants in a circle. The pink circle signifies that this enemy ant hill will be destroyed in a few rounds.

Defenses
One algorithm I implemented early on, before I had a decent combat algorithm, was static defenses. Depending on the number of ants I had, I would place ants next to my hill as long as at least 2 directions where free to move to from on top of the hill. This helped a great deal to defend against bots without combat intelligence, but was useless against bots in the top 100.
However, the day of the bot submission deadline, I removed this and instead gave enemy ants a higher potential the closer they come to my hills. On top of that, I define suicide zones near my hills, meaning that if any enemy ant get into these zones, my ants are allowed to suicide to kill them.
The net effect is that I have a bit more ants early game to explore and gather food, since otherwise the static defender ants would just sit there. Perhaps more importantly, due to the increased potential of enemy ants near my hill, attackers are pushed away. Less sophisticated bots aren’t even able to get close enough to see my hill and thus don’t try to destroy it at all.
Although it is dangerous to add lots of new code near the deadline, all the tests I ran on the last day seemed to indicate that my bot with these changes did a lot better than the previous version without, so I kept them in, hoping no bugs would pop up.
Symmetry detection
One peculiarity of the maps that I haven’t mentioned so far, is that they are all symmetric. This means that, with any given base, 17 different maps can be generated, as per the wallpaper group definition. If you manage to find the base from which a map is generated, you can infer the location of enemy hills and food spawns in unseen areas of the map.
Clearly, being able to do that can lead to a big tactical advantage. Therefore, I tried to have my bot do symmetry evaluation. It does not detect all possible types of symmetry however, only tilings (so no rotations or reflections). Due to a lack of time, and an inefficient approach towards symmetry detection, I did not manage to add detection of all possible symmetries.
If the bot detects symmetry and no enemy hill is currently being attacked, but one has been seen or destroyed in the past, an artificial hill is added at the correct, inferred location. As soon as an actual hill is seen, this artificial hill is removed again. This ensures that, assuming a symmetry is found, as soon as my ants destroy a hill (or an enemy destroys a hill I’ve seen), my ants will move on to the next enemy hill using the shortest path, even if they have not seen it yet.
I wait to add these artificial hills until an actual hill has been seen to make sure that there are enough ants to start attacking hills. If I add the artificial hills as soon as I detect symmetry, I often only have around 10-20 ants and attacking then would kill too many ants that could be gathering food. Trying to come up with a better method of when to add hills lead to nothing, as it is quite hard to estimate how well you are doing compared to the enemy players, since large parts of the map are often not visible to the bot.
An example of symmetry detection at work is shown below. In this image, the orange overlay is the area my ants can’t see. The dark bars on the sides is where the map wraps around. Light blue tiles are water tiles that have either been seen or inferred. You can see that, even though my ants have explored less than a third of the map, most of the water tile locations are already known. The direction of symmetry is shown by the red arrow in the bottom left corner.

Optimizations
Even though I code in C++11, which is regarded as one of the fastest languages, I still need speedups to ensure I do not time out (i.e. take more than 500 ms calculation time per round). The most important thing when optimizing is definitely to use some kind of profiling tool. My preference goes towards Callgrind (which is part of Valgrind in combination with KCachegrind, which I find much better and easier to use than the text-based gprof.
There’s two parts in my code where optimizations lead to large speed gains. First of all, the diffusion. The ants behave better the more diffusion steps are calculated, so it is important to be able to do as many diffusion steps as possible within one turn. In order to do this, I cached lots of fixed variables, removed all function calls, changed branches to tertiary operators, minimized the number of mathematical operators by reordering and grouping calculations, and split up my diffusion loop in such a way that I didn’t have to take into account coordinate wrapping anymore. This transformed my diffusion function from ±15 lines to a ±250 lines monster, but gave me a 50× speedup. Doing 200 diffusions on a common 50×175 map takes around 130 ms and on a 196×196 map it takes around 310 ms, which leaves more than enough time for other calculations. Just to make sure timeouts don’t happen on extremely large maps, the bot checks its remaining round time every few diffusion steps.
The other part of the bot that was slow was the combat evaluation. One single (map-wide) evaluation was super fast, somewhere around 3 ms, but due to the fact that I completely reevaluate the combat situation after moving every single one of my ants, it was not unusual that the bot needed 200 ms to get the final positions for all ants in combat. Clearly this part required some speedup.
First of all, instead of completely reevaluating the combat resolution, I only do so for ants that could have their combat evaluation results altered due to the move of the ant which position I fixed. This was quite involved, requiring a lot of extra storage in order to keep track of which ants influence which tiles. Luckily, storage is a lot less of an issue than calculation speed.
I also implemented a bucketed priority queue to keeping track of the strength of enemy ants. It seems this type of queue is also used in some OS schedulers, path finding algorithms, etc, but I had a hard time finding any real info on it. Instead of a heap-based priority queue, such as the standard C++ one (which was too limited in its functionality in this case), you use a hash map, mapping priority to a hash set, and store all objects for a certain priority in the hash set. So the definition of the priority queue variable is:
std::unordered_map<size_t, std::unordered_set<containedType> > bucketedPriorityQueue;Almost any function on this type of queue has — in general, not worst case! — a run time of O(1): getting minimum and maximum priority, updating object priorities, inserting & removing objects,… For some of those functions, some helper data is required. The queue should use lazy initialization, i.e. it should only create a hash set for a certain priority if an object with that priority exists. If this is not done, it’s quite slow to instantiate. Overall, I’m very impressed by this type of priority queue and can’t quite understand why it’s so hard to find information on them.
The combination of doing only local updates during combat evaluation and using the lazy initialized, bucketed priority queue made total combat resolution times drop down from 200 ms to 5–10 ms, a 20–40× speedup.
Final remarks
Even though I did a ton of tests, some bug still managed to find its way into my code. When the bot plays on a map where no water tiles are visible, it will always move its only ant north. After this one move, if still no water tile is visible, the single ant will just stay where it is. No timeout, no crash, nothing… I only noticed this 2 hours before the submission deadline and didn’t want to risk breaking something else by fixing it, so I left it in. There there are few maps on which the bug triggered during the final competition which decided the ranking, but I don’t think it influenced my final position. Next time though, I should test more thoroughly and probably refrain from introducing big changes during the last 24–48 hours before the deadline.
In the end, despite losing a few games due to the bug, I managed to reach the 53th position out of 7897 contestants, not bad!
Looking back on the competition, it was a great way to refresh my AI knowledge and a fantastic learning experience. I would like to thank Memetix, a1k0n, delineate, icefox, mathiasds & Nefbrethilion for all their shared ideas. Without them, my bot would not have anywhere near the skill that it has now.
